The most fundamental equation in mechanics , derived on the basis of absolute truths (derivation shown below), makes it really inevitable to recognize the fundamental discrepancy hampering clasical physics, deeply penetrating it and causing the unnecessary appearance of the physically deformed view of nature brought about by quantum mechanics. Here, the word is about the fundamental misunderstanding in classical mechanics of the concept of motion.

Indeed, Newton's second law , which is an expression of Newton's third law, especially if it's written as to reflect the fact that the force invokes a compensating equal in magnitude but opposite in direction inertial counterforce . The application of such force on the body cannot change the state of the body as required by Newton's first law and invoke motion. Force only causes matching to appear.

Furthermore, the free body under the action of the constant force cannot undergo real displacement and a claim that work A has been done on the body is unsustained: .

Another direct demonstration that mechanics treats incorectly as equations of motion equations describing rest is seen in the most general equations of mechanics -- Hamilton's equations. Not only is Newton's second law derived from Hamilton's equations but they serve as the basis to form the quantum mechanical operator called the Hamiltonian. Therefore, quantum mechanics possesses the flawed birthmarks of classical mechanics. They are passed on to quantum mechanics.

   and         (7)

Now, if conservation of energy is in effect, as physics accepts, then, . Therefore,

   and         (8)

Hence,

   and         (9)

In other words, if conservation of energy is to be obeyed then the body must be at rest.

The Most Fundamental Equation in Mechanics

After the obviously necessary abandonment of quantum mechanics, the comporting of classical mechanics with the scientific method and its further development along the road of truth and reason must begin with recognizing the imprtance of an equation, elevated by this author as the most fundamental equation of mechanics when treating a free body under the action of a constant force.

It is not appreciated so far that an equation, which sometimes is used in university physics exercises and which stems from the absolute truths of physics, is in fact the most fundamental equation of mechanics, inherently containing the so far neglected proper treatment of motion when a constant force acts on a free body.

That most fundamental equation shows directly that when a real displacement of a free body occurs under the action of a constant force, there must necessarily be a change of velocity of that body, an inescapable fact blanketly disregarded in physics. This follows from the absolute truths of physics. Absolute truths of physics are, for instance, its definitions.

Thus, it's an absolute truth that velocity is

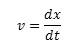     (10)

Also, it's an absolute truth that acceleration a is

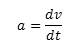     (11)

From these two definitions we can express dt in two ways

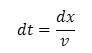     (12)

and

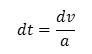     (13)

Now, these two expressions being equal, allows us to write

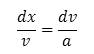     (14)

or, reordering it

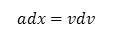     (15)

which may also be written as

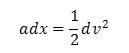     (16)

Now, we can integrate both sides of this equality

     (17)

factoring out of the integral the constant acceleration a as well as the constant one half. From where we get

     (18)

Finally, we have

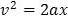     (19)

This equalion of a parabola, has come about from absolute truths of physics. Therefore, the connection between the velocity v, acceleration a and the position x is set in stone and is also an absolute truth. We now can plot it and see what conclusions we can get from it.

For simplicity, we will take the acceleration to be . Thus, the parabola becomes: and the plot appears as follows: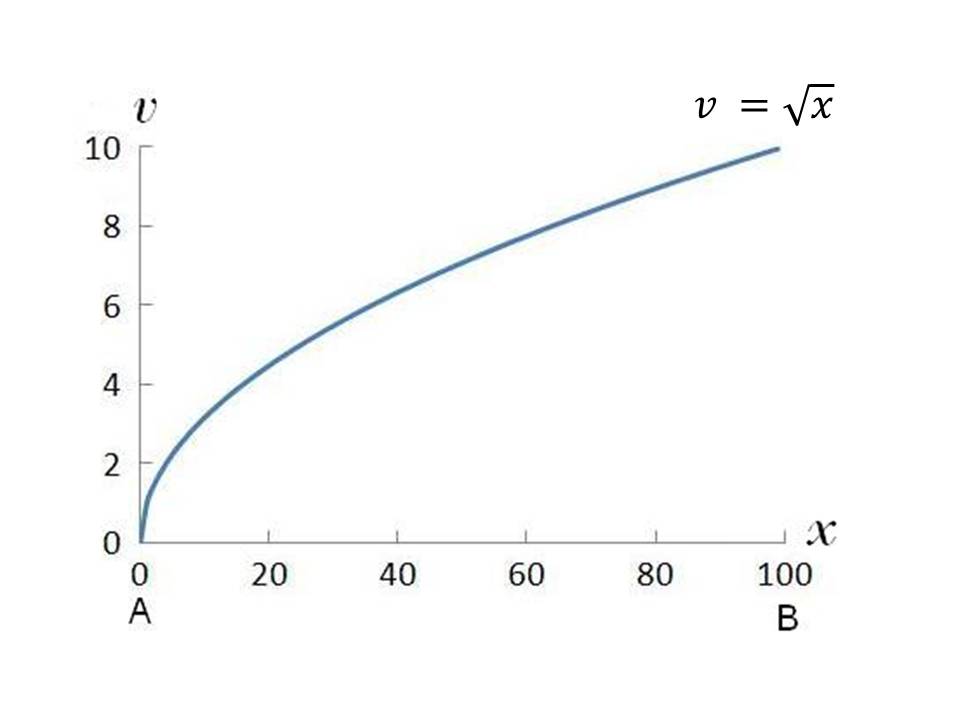

It is seen from the above that the graph of as a function of square root of x is only an idealized plot, which considers that acceleration is valid for any velocity, no matter how high. However, as seen, as the velocity gets higher, the constant acceleration becomes less and less significant and for some high velocities it becomes so small in comparison that it can be neglected. In other words, the velocity attains a constant value, reaching the clasical velocity limit.

Now, one may wonder, didn't I say that kinetic energy is the measure of motion at high velocities but, on the other hand, didn't I say that when at these high velocities the velocity becomes constant, that means that the body is in uniform rectilinear motion, which I also said, is akin to rest.

There's no contradiction.at all because from the point of view of the body (for an observer at rest with the body), its state will indeed be akin to rest. There's no experiment that can be performed in the coordinate system attached to the body to prove that the body is not at rest but is in uniform rectilinear motion. The coordinate system attached to the body will be an inertial system. It will have no acceleration.

On the other hand, for a stationary observer outside of the body, with respect to whom the body is moving at the said constant velocity, the body will be in motion, specifically in uniform rectilinear motion, and it will possess kinetic energy dependent on its mass and its constant velocity.

When one looks at the above-shown graph of , one may wonder how is the velocity reaching a plateau. A parabola, such as the one shown, doesn't have an asymptote. This is one of these moments when we should remember that mathematics is only a helping tool in physics. It's the physical reality which determine the conclusions. Thus, in this case we should come to realize that numerically, when the velocities become very high, they dwarf the constant acceleration. Therefore, acceleration can be neglected and, therefore, force loses meaning. This can be seen immediately from the complete expression of Newton's second law:

     (20)

where the negligible acceleration makes the first term after the equality disappear. The second term after the equality, being equal to the first term (following from the most fundamental equation of mechanics), is also negligible. Therefore, the whole expression for the real force vanishes. Force has no meaning at high velocitites attained when a free body initally at rest is acted upon by a constant force.

On the other hand, if we use the complete Newton's second law to express the work needed to drive into motion the free body acted upon by a constant force:

     (21)

we see that none of the terms on the right side of the equality can be neglected -- firstly, because the second term contains the ever increasing positive value of velocity, squared at that. Secondly, because the first term after the equality sign is equal (following from the most fundamental equation of mechanics) to the non-neglectable second term .

Further, that sameness of the two terms after the equality sign allows us to write the above equation as:

     (22)

which yields

     (23)

or finally

     (24)

As for the equation , eq.(22), it shows that even at low velocities the motion of a free body under the action of a constant force can be expressed in energy terms; that is, two times kinetic energy. Similar to the finding thst the complete Newton's second law is and not just .

Of course, by utilizing the fact that the two terms after the equality sign of are equal we may write it this way (considering also , for simplicity, that )

     (25)

or

     (26)

This way of expressing energy conceals the origin of the motion causing the displacement and only states that had there been such displacement of the mass m, it would have required energy equal to the product of the mass and the displacement itself. So, again, we must consider the physical meaning of what was derived mathematically.

This also demonstrates the equivalency rather than transformation of other quantities into energy. Thus, only means the energy has its equivalent expression in terms of mass and not that mass can be transformed into energy. The same way, shows another equivalent expression of energy for low values of , where acceleration is still not negligible.

Author's email: qmiscm@hotmail.com